by Andrew Kliman
Ted Reese, The End of Capitalism: The Thought of Henryk Grossman.
Winchester, UK and Washington, USA: Zero Books, 2022.
Henryk Grossman was fortunate. The book in which he propounded his breakdown theory of capitalist economic crisis was published just months before the Great Depression erupted.
Ted Reese is not fortunate. His book, which staunchly defends Grossman’s breakdown theory, has been published just months after I showed that the theory is fatally and irreparably flawed.
Reese’s book is similarly flawed, but the blame ultimately does not rest with him. He was playing a poor hand.
Contents
One chapter of Reese’s book presents and endorses Grossman’s breakdown theory. In addition, the introduction and the final chapter take up a variety of recent economic events and trends––regarding debt, finance, and money; economic growth and crisis; automation; and other matters––construing them as manifestations of the supposed breakdown tendency. The discussion drives toward a conclusion that is apocalyptic yet carefully hedged, an awkward combination: “capitalism … may well be entering … its ‘final breakdown’”; the book applies “Grossman’s thought … to the present––quite possibly, final––capitalist crisis”; “capitalism may have entered the process of a breakdown it cannot recover from” (pp. 1, 2, 5).
Two chapters survey Grossman’s life, thought, and political activity. The first covers the period up to 1929, when he published The Law of Accumulation and Breakdown of the Capitalist System, which spelled out the breakdown theory. The second covers the remaining 21 years of Grossman’s life. Another chapter summarizes six shorter works by Grossman, written between 1926 and 1943. These three chapters draw extensively on the work of Rick Kuhn, the world’s leading Grossman scholar.
Background
Grossman’s breakdown-theory book showed that capital accumulation could not continue indefinitely if variable capital (which pays workers’ wages and benefits) and surplus-value (profit) were to continually increase at one fixed rate, while constant capital (accumulated investment in means of production) were to continually increase at a higher fixed rate. The persistence of these growth paths would eventually require that new investment in constant and variable capital exceed the funds available for investment––that is, the profit––and thus capitalists’ personal income would plunge into negative territory. Yet before that occurred, capitalists would (temporarily) halt the capital accumulation process, which would trigger an economic downturn.
Grossman understood that this growth model is seriously flawed. Originally developed by Otto Bauer (but only for a four-year time span), Grossman adopted it provisionally, to show that it eventually leads to breakdown. He then modified some of Bauer’s assumptions and simplifications, including the assumption that generates breakdown (fixed-but-unequal growth rates of constant and variable capital). Yet Grossman did so only verbally; he did not incorporate the modifications within the formal model. This proved to be a fatal error. It led him to conclude, wrongly, that although the modifications can cause the moment of breakdown to be postponed, they cannot eliminate the breakdown tendency.
Bauer’s assumption that constant and variable capital increase at fixed-but-unequal rates was a way of modeling continuous technical change: means of production increase more rapidly than employment of workers. But means of production and constant capital are not the same thing; the former are physical things, while the latter is a sum of value. As Grossman recognized clearly, once we assume continuous technical change, it is untenable also to assume that constant capital grows as rapidly as means of production. The productivity increases brought about by technical change tend to reduce the prices of means of production, and thus the sum of value invested as constant capital tends to increase more slowly than investment in physical means of production.
When this occurs, does constant capital still permanently grow more rapidly than variable capital and profit? And thus, is a moment of breakdown still inevitable, even though it has been postponed? Grossman said yes, but his answer, evidently grounded in nothing firmer than his intuition, was incorrect. My recent article on his breakdown theory demonstrated that if, as he assumed, Marx’s value theory holds true, and employment of workers and the new value they create increase over time, then there is no possible time path of capital accumulation that generates a breakdown tendency in the long run. Rising productivity cheapens means of production to such an extent that constant capital ultimately grows at the same rate as variable capital and profit, not a higher rate.[1]
Prior to the long run, a Grossman-style breakdown is still logically possible. However, the cases in which it could occur are highly implausible––cases in which physical output is constrained to grow more slowly than physical investment (in means of production plus workers’ consumption goods) or in which capitalists invest more than 100% of their profit.
Reese on Grossman’s Breakdown Theory
Reese’s discussion of the breakdown theory is uncritical. Only two pages are devoted to criticisms of the breakdown theory, and they do little more than summarize a couple of Grossman’s own responses to early critics. The only criticism that engages Reese’s interest is the charge that the breakdown theory is mechanical (which he denies). He seems to treat the substance of the theory, especially its logic, as unproblematically correct.
After asking whether any of the needed modifications of Bauer’s original model “suppress the breakdown tendency altogether,” Resse provides “a logical shortcut to the answer: … any counter-tendencies that emerge spring from the primary tendency. The breakdown tendency and the counter-tendencies are part of the same piece of elastic” (p. 54, emphases in original). I do not understand the metaphor, and I do not see that the emergence of the counter-tendencies from the “primary” tendency resolves, or even addresses, the question at issue: which of them is stronger?
In any case, Reese stated his view clearly in a Cosmonaut Magazine article last year: “Ultimately, Grossman found that no counter-tendency suppresses overaccumulation [and breakdown] for good.” “Ultimately, Grossman shows that all of the counter-tendencies must eventually exhaust themselves.”
With respect to the crucial issue––the extent to which rising productivity reduces the values and prices of means of production, and, consequently, the extent to which the growth of constant capital falls in relation to the growth of means of production––Reese has little to say. Apart from quoting Grossman on the matter, he says only that
[i]nnovations demanded by accumulation devalue labour power, commodities and capital, so the assumption of constant values cannot be maintained. The quantity of surplus value is calculated against a reduced capital value. The rate of valorisation rises and delays the breakdown tendency. [p. 54]
But this, too, simply summarizes what Grossman himself said.
The key words are the four final ones: “delays the breakdown tendency.” Grossman claimed that the breakdown tendency can only be delayed, not eliminated, when rising productivity causes the values of means of production to fall. Yet despite what Reese’s Cosmonaut Magazine article stated, Grossman did not find, or show, that this claim is correct. He merely asserted it, without any accompanying argument, and he was incorrect.
Reese’s Zero Rate of Profit Tendency
There is one respect in which Reese’s theorizing seems to move beyond Grossman. On the one hand, he reiterates Grossman’s argument that breakdown is ultimately inevitable because the amount of surplus-value generated in production is ultimately too little to permit capital accumulation to continue along its growth path without disruption. On the other hand, Reese offers an additional argument for the ultimate inevitability of breakdown. He contends that variable capital, as a share of total capital, approaches zero over time and, consequently, the rate of profit likewise approaches zero over time.
These conclusions are indeed implications of the fixed-but-unequal growth rate assumption that Grossman provisionally took over from Bauer. However, I am not aware that Grossman thought that they still hold true after the needed modifications to Bauer’s model have been made.
Reese introduces his explanation of the breakdown theory by means of the following argument:
constant capital … tends to grow relative to variable capital …. For if variable capital alone returns new value but shrinks relative to constant capital, then it is clear that the share of the value-creating component in the organic composition of capital (constant capital plus variable capital …) tends to shrink proportionally and historically towards zero.
That constant capital grows relative to variable capital is obvious –– … the means of production (M) grows [sic] relative to living labour (L) ….
When labour-saving technology reduces total labour time … per commodity, … there are fewer workers relative to the total amount of the now expanded machinery, [so] the contribution of the value-producing component, variable capital, shrinks relative to constant capital. [pp. 35, 36, 37–38; emphases altered]
This chain of reasoning leads him to conclude that the rate of profit, too, is inevitably falling toward zero over time.
However, the chain of reasoning is flawed, and its conclusions are incorrect. First, it is wrong to try to infer the growth of constant capital directly from the growth of means of production. As I discussed above, the “labour-saving technology [that] reduces total labour time … per commodity” tends to reduce the prices of means of production. This offsets, to some extent, the physical increase in means of production, so constant capital does not increase as rapidly as the physical volume of means of production.
In principle, the price reductions can be great enough to fully offset the physical increase in means of production. In that case, even though “there are fewer workers relative to the total amount of the now expanded machinery,” there are not fewer workers relative to constant capital.
Yet generally, the price reductions will not fully offset the physical increase in means of production, so constant capital will indeed increase in relation to variable capital. But by how much? For how long? And, most importantly: even if constant capital increases in relation to variable capital forever, is that increase limitless?
Reese’s argument can be correct only if the increase is indeed limitless. To see that it otherwise does not go through, imagine that constant capital rises from 36% of total capital to 54%, 66%, 74%, … of total capital––moving ever-closer to, but never surpassing, 90%. So variable capital, which is originally 64% of total capital, continually falls as a share of the total, but never below 10%. In other words, “the share of the value-creating component,” variable capital, does not “tend[ ] to shrink proportionally and historically towards zero” (emphasis added).
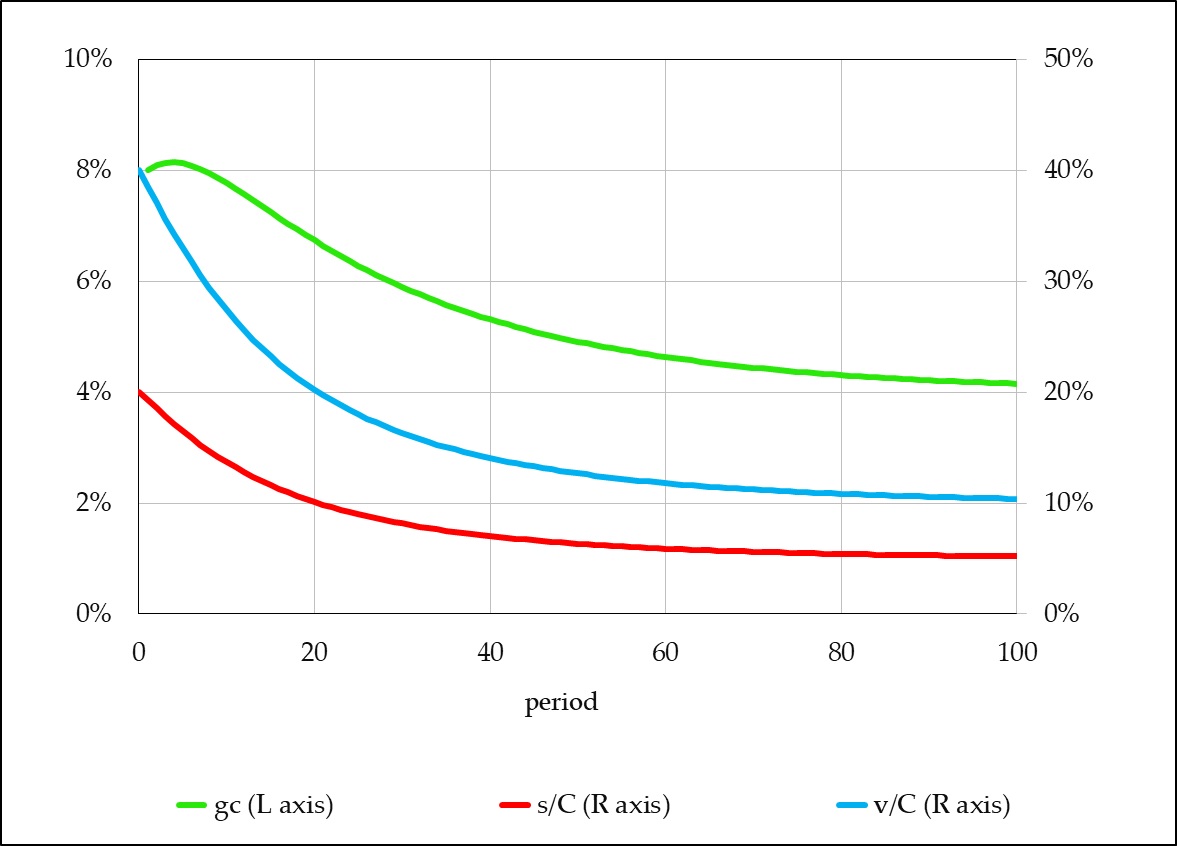
Consequently, the rate of profit does not fall to zero over time. It eventually settles at a level equal to 10% times the rate of surplus-value. (If C is total capital, s is surplus-value, and v is variable capital, then the rate of profit is s/C, variable capital as a share of total capital is v/C, and the rate of surplus-value is s/v. Since s/C ≡ (v/C) × (s/v), the rate of profit is variable capital as a share of total capital times the rate of surplus-value.)
The case we have just considered is not some bizarre exception. It is the rule. No other case is remotely plausible. Indeed, if the absolute amount of profit (surplus-value) rises over time and capitalists do not accumulate more than their total profit as additional (constant and variable) capital, then accumulated capital simply cannot increase limitlessly relative to profit. It can increase, and increase forever, but there is a definite upper limit to the ratio of capital to profit that cannot be surpassed. Putting the same thing differently, there is a definite (and positive) limit below which the ratio of profit to capital––the rate of profit––cannot fall.[2]
Here’s why: no matter how much the physical means of production increase, the newly accumulated capital (in terms of value) is a portion of the latest period’s profit, and thus the growth of capital-value is constrained by the growth of profit. In the long run, capital-value cannot grow more rapidly than profit. As the share of profit that is accumulated approaches its maximum value (either 100%, the theoretical limit, or some lower limit that exists for practical purposes), the growth rate of capital-value approaches the growth rate of profit. This is the key point that has escaped the attention of the devotees of the Grossman breakdown model––just as it escaped the attention of Grossman himself, when he asserted incorrectly that the cheapening of means of production can only postpone, but not eliminate, his breakdown tendency.
But if capital grows only at the same (percentage) rate that profit grows, then the rate of profit is no longer heading downward. It has reached the lower limit, below which it cannot fall.
Interactive spreadsheet example, illustrating the propositions demonstrated above. Users can alter the values of several parameters and initial conditions and see how the changes affect the results.
Reese’s Evidence
Reese also tries to marshal empirical evidence to support his conclusion that the rate of profit is inevitably trending toward zero. Yet a theoretical conclusion that cannot possibly be true does not become truer just because the evidence may seem to confirm it. Evidence can never actually confirm false claims. Once we know they are false, we also know that they are being “confirmed,” not by the evidence itself, but by some combination of misinterpretation of, unwarranted inferences from, and cherry-picking of the evidence, as well as disregard of other possible interpretations of the evidence.
I cannot possibly review all the evidence here. I shall limit myself to two examples.
One bit of evidence that Reese regards as particularly important is Esteban Maito’s estimate of the rate of profit in high-income countries. He reproduces Maito’s graph and adds the caption, “The general rate of profit falls historically towards zero, meaning capitalism must end” (p. 142). Reese also writes, “As of 2014, it is on course to reach zero around 2054” (p. 141), because 2054 is when the rate of profit reaches zero––on the trendline that Maito drew through his data. Leaving aside serious questions about Maito’s concept of the “rate of profit” and the methods he used to combine data from different countries, the problem here is that he explicitly warned that his linear extrapolation from the data cannot properly be interpreted as a forecast: “Although the 0% profit rate should not be regarded as the real limit of capital, but higher levels [of the profit rate are the real limit], the years which the trend line reaches 0 % were considered” (pp. 17–18 of Maito’s PDF document).
Maito’s warning was appropriate. The 2054 value of the rate of profit on his linear trendline is not evidence that the rate of profit will fall in the future until it reaches zero. It is not a data point. It is merely the answer to a “what if?” question: “What if the rate of profit were to continue to fall, linearly, until it reached zero? When would it do so?” To regard the 2054 value as something more than the product of pure speculation, one first needs to assume that the rate of profit will fall to zero. And that is what Reese is doing here, assuming his conclusion.
Shortly after this misinterpretation of Maito’s trendline, Reese reproduces a graph of global Gross Domestic Product (GDP) between 1913 and 2015, which rises almost 23-fold, and he appends the caption, “The ever-steepening trajectory of accumulation indicates the eventual inevitability of an absolute historical limit” (p. 144). Setting aside the fact that GDP growth and capital accumulation aren’t identical, how exactly does the graph “indicate” anything about the future, especially the “eventual inevitability” of a maximum level (of GDP or of accumulated capital) that cannot be surpassed?
The rise in global GDP looks unsustainably great to Reese only because of the preconceptions he brings to the data, not because of anything untoward about the data themselves. (As Abraham Maslow famously remarked, “If the only tool you have is a hammer, it is tempting to treat everything as if it were a nail.”) The 23-fold rise in global GDP works out to a fairly modest 3.1% average annual increase, and GDP per capita rose by just 1.6% per year on average during this period. If there is any actual evidence that these growth rates cannot possibly be sustained in the long run––not just speculations and Grossman’s flawed breakdown theory––the book does not provide it.

Grossman vs. Marx
Reese comes close to equating Grossman’s theory of capitalist economic crisis––the breakdown theory––and Marx’s crisis theory. “Marx’s true economics could have been lost for good without [Grossman’s] contribution …. He must be rehabilitated” (p. 11). “It is not too late to put Grossman alongside Marx at the heart of scientific socialism––doing so would ensure that Marx really is at its heart” (p. 153). His Cosmonaut Magazine article of last year was, if anything, even more effusive, suggesting that Grossman’s 1929 breakdown-theory book reclaimed not only Marx’s true crisis theory, but pretty much everything of value in Capital. It “did the best job after the deaths of [Marx and Engels] of defending and clarifying the real, revolutionary content of Marx’s Capital.” It “serves as a kind of sequel (as well as a very good primer) to Capital, highlighting and elaborating its most important findings.”
However, the book does not make a serious effort to support these claims. It contains some scattered references to what Marx said about value, economic crisis, and capitalism’s crisis tendencies, but there is no sustained engagement with his theory, nor is Marx’s crisis theory considered in and for itself. Reese turns to Marx mainly to shed light on Grossman’s theory.
Reese’s interpretive practice is at times rather creative. For example, when discussing his claim that the rate of profit approaches zero, he suggests that a passage in Marx’s Grundrisse anticipated the claim. Reese writes:
the general rate of profit in the “high-income countries” … is on course to reach zero around 2054. As Marx wrote in Grundrisse, published in 1858:
As soon as labour in the direct form has ceased to be the great wellspring of wealth, labour time ceases and must cease to be its measure …. Capital thus works towards its own dissolution as the form dominating production. [p. 141; ellipsis in quote from Marx is Reese’s]
Yet I think the main problem with Reese’s treatment of the Marx-Grossman relation is that he does not investigate the possibility that their crisis theories might differ in significant ways. He treats their theories as one and the same, even though Grossman himself criticized Marx. Grossman took issue with Marx’s emphasis on the tendency of the rate of profit to fall, rather than on the “fact” that the mass (i.e., absolute amount) of profit is ultimately too little to allow capital accumulation to proceed without disruption. He also criticized Marx for having failed to demonstrate the existence of a breakdown tendency. Further investigation of these issues would have revealed that Grossman’s criticisms reflect theoretical differences. In contrast to his own theory, there is no moment in Marx’s theory when the mass of profit is insufficient in the above sense and, accordingly, no moment of breakdown or tendency toward breakdown caused by such insufficiency.
For Grossman, and for later devotees of his breakdown theory, a main attraction of the theory is the alternative to reformist theory and politics that it provides. Yet the breakdown theory and reformism are not the only alternatives. As I discussed in my recent article, the fact that Marx’s crisis theory differs from Grossman’s breakdown theory does not make it reformist. Its political implications are revolutionary, even though they are not based on insufficient profit (in the above sense) and the associated breakdown tendency, but on other factors.
If the breakdown theory has been shown to be fatally flawed, as I contend, the fact that Marx’s crisis theory rests on different bases is a good thing! Revolutionary thinkers would do well to consider it anew––in and for itself, instead of through the lens of the breakdown theory.
Endnotes
[1] More precisely, constant capital ultimately grows at the same rate as new value. The latter can be decomposed into variable capital and profit. If profit grows faster than variable capital, this does not affect the growth of new value, but it does lead to an even-greater reduction in the gap between the growth of constant capital and the growth of profit.
[2] Let gs ≡ Δs/s and gC ≡ ΔC/C denote the percentage growth rates of surplus-value and (total) capital, respectively, and let a = ΔC/s denote the fraction of surplus-value accumulated as additional capital. Δ stands for “the change in.” Assume that surplus-value increases over time, so that gs > 0 , and that capitalists do not accumulate more than the total surplus-value as additional capital, so that a < 1 .
Since a = ΔC/s , ΔC = as . And since a < 1 , ΔC cannot permanently increase more rapidly than s . But as long as gC > gs , C does increase more rapidly than s . Thus, if gC > gs , C must eventually increase more rapidly than ΔC . But ΔC and C are the numerator and denominator of gC , respectively, so gC must eventually decrease. The process repeats as long as gC > gs , until the point where gC = gs . In other words, gC converges to gs .
But gC ≡ ΔC/C = as/C , so gC = gs implies that gs = as/C , and therefore that the rate of profit, s/C , equals gs / a . Thus, as gC converges to gs , the rate of profit converges to gs / a ––which must be positive, not zero, since gs > 0 and a < 1 . And since s/C ≡ (v/C)(s/v) , it follows that v/C converges to (gs / a ) ∕ (s / v) .
The propositions demonstrated above are illustrated in the interactive spreadsheet example that accompanies this review-essay. Users can alter the values of several parameters and initial conditions and see how the changes affect the results.


Be the first to comment