
by Andrew Kliman
Traducción al español de A. Sebastián Hdez. Solorza: “La utilidad marginal negativa de la ‘Respuesta a Andrew Kliman’ de Rallo”
Negative marginal utility is where you have too much of an item, so consuming more is actually harmful.—Investopedia
On April 13, Juan Ramón Rallo published his “Reply to Andrew Kliman”—a response to my September 4, 2024 article, “Rallo’s Anti-Marx Critique of Marx and the TSSI”—on his Substack blog, Utilidad marginal (Marginal utility). He really should rename it Utilidad marginal negativa (Negative marginal utility), because his reply to me is just too much.
Ángel Barroso promptly called out Rallo for quoting a passage in my critique
out of context and completely distorting the original meaning. … He portrays Kliman as if he were admitting that the Marxist transformation problem has no solution, when in fact he is saying something very different. … [W]hat Kliman proposes here is not a renunciation of value theory or a recognition that the transformation problem is insoluble. What he does is criticize the way in which Rallo … formulate[s] the problem: demanding logically incompatible conditions.
This was not an isolated instance. As I will discuss below, Rallo’s reply contains numerous significant misrepresentations, not only of what I have written, but of what was written by the brains behind his whole operation, Ladislaus von Bortkiewicz.
I greatly appreciate Barroso’s intervention to set the record straight, and I agree in the main with his critique of neoclassical economics and his defense of the temporal single-system interpretation of Marx’s value theory (TSSI). However, my own critique of Rallo’s reply will be quite different from Barroso’s, for two reasons. First, the debate between Rallo and Barroso did not focus on what I think is the all-dominating, fatal defect in Rallo’s reply to me, its failure to understand that the TSSI is a single-system interpretation.
Second, I will not focus on my methodological or epistemological differences with Rallo, as Barroso does. While I am certainly no proponent of the static-equilibrium reasoning that Rallo employs or the ideology such reasoning expresses, Marx’s theory and the TSSI can be right only if they are compatible with all cases in their domain, without exception—including a state of static equilibrium. So I will focus on showing that Rallo is wrong to claim that they are incompatible with that (very special and wholly hypothetical) case.
The first six sections of this article establish that Marx’s aggregate value-price equalities hold true (given his premises), and that the TSSI preserves the aggregate equalities, in all cases, including the case of static equilibrium. In these sections, I also argue that the reason Rallo denies this is that he fails to understand that the TSSI is a single-system interpretation.
The final four sections deal with Rallo’s have-it-both-ways argumentation. He imposes restrictions that make both “Marx’s” account of the value-price transformation, and Bortkiewicz’s “correction” of Marx, incompatible with simple reproduction.[1] Rallo rejects “Marx’s” account and its aggregate equalities because it violates simple reproduction, while endorsing Bortkiewicz’s “correction,” even though it also violates simple reproduction! Rallo argues that it does not, but I demonstrate that his account of Bortkiewicz’s procedure is a blatant falsification. After considering various possible ways to make the “correction” compatible with simple reproduction, I conclude that they must fail because, when prices change, Rallo’s input-substitution restriction is simply incompatible with simple reproduction.
1. Background
A commodity’s price almost never equals its value. Accordingly, a business’s profit almost never equals the surplus-value it pumps out of its workers. Real-world prices and profits thus seem to be incompatible with Marx’s value theory. But Marx argued that, in the economy as a whole, the sum of the prices equals the sum of the values, and the sum of the profits equals the sum of the surplus-values. And a third equality follows immediately from these two: the economy-wide “price” rate of profit (profit divided by invested capital) equals the “value” rate of profit (surplus-value divided by invested capital).
In light of these aggregate value-price equalities, Marx concluded that the supposed incompatibility between his theory and the facts is only apparent, not real. Despite the myriad deviations of price from value, the aggregate price of output is determined by the aggregate value of output, and aggregate profit is determined by aggregate surplus-value. When the “law of value” is understood properly, as a law of the aggregate economy, it is consistent with the real-world facts.
However, the anti-Marx crowd has claimed for more than a century that his argument is internally inconsistent. It has also claimed that, when this alleged error is corrected, the aggregate value-price equalities cannot all be preserved. Ladislaus von Bortkiewicz supposedly proved that Marx’s argument is internally inconsistent, and Bortkiewicz’s “correction” of Marx became the template for the ones that followed.
Yet the actual error here is the anti-Marx crowd’s misinterpretation of Marx’s argument. According to the temporal single-system interpretation of Marx’s value theory (TSSI), his actual argument was radically different from the one they attribute to him. When we interpret his argument correctly, Marx’s conclusions follow logically from his premises; the alleged inconsistency simply vanishes.
Thus, there is nothing to correct. And thus, the aggregate value-price equalities are preserved.
Rallo is desperately seeking to overturn this result. He wants to concoct a special case in which Marx’s aggregate value-price equalities cannot be preserved, even when his argument is understood in accordance with the TSSI. Rallo will not find such a case, because there is none.
I explained this to him, at some length, in my critique of his Anti-Marx:
given the data that Marx used[,] … prices of production can always be computed …. The computations always lead to the conclusions that total profit equals total surplus-value, and that the economy-wide total price of all industries’ products equals their total value.
Note that the data that Marx employed in his computations are enormously different from the data with which Bortkiewicz and all other simultaneist theorists begin. There is no assumption that simple reproduction takes place. Physical input-output relations are not among the data, nor are physical quantities of any inputs or outputs. Marx does not force input prices to equal subsequent output prices.
The reason none of these things are among his data is that they are irrelevant, given his concept of prices of production and his theory of what determines their magnitudes. To compute these prices, we only need to know the period’s capital investments, components of cost prices, and surplus-values. …
In short, Marx’s procedure is entirely general. It does not rely on any restrictive assumptions whatever. [Emphases in original.]
Despite this explanation and clear warning that any attempt to falsify the aggregate value-price equalities is a fool’s errand, Rallo is adamantly clinging to his job as fool’s-errand boy. Because he seriously misinterprets the TSSI, he refuses to understand that there is no special case in which the TSSI fails to preserve the aggregate equalities. It is true that the TSSI as misinterpreted by Rallo cannot preserve the aggregate equalities, but that is an entirely different matter.
2. Marx’s Actual Argument
If we consider Marx’s actual argument (as understood by the TSSI), instead of Rallo’s misinterpretation, it is extremely easy to prove that the aggregate equalities hold true, without any exception whatsoever. In any period, the value of the output of any sector, j, is
(1) Wj = Cj + Vj + Sj
where C (constant capital) is defined as the actual cost of the means of production that were consumed in the production of the output, V (variable capital) is defined as the actual cost of hiring the workers who produced the output (i.e. their actual wages and benefits), and S is surplus-value. Because the TSSI is a single-system interpretation, there is only this one constant capital and this one variable capital. There is not a separate “value system” in which commodities exchange at their values. Thus, there is no separate constant capital that equals the value of means of production and no separate variable capital that equals the value of the goods that workers consume.
Since C and V are actual costs, the price of the output of sector j is the sum of these costs and the sector’s profit, π:
(2) Pj = Cj + Vj + πj
So the economy-wide sums are
(1´) ∑Wj = ∑Cj + ∑Vj + ∑Sj
(2´) ∑Pj = ∑Cj + ∑Vj + ∑ πj
In chapter 5 of Capital, volume 1, Marx demonstrated that, when commodities exchange at prices that differ from their values, this changes only the distribution of the already-existing value; it does not alter the total amount of value in existence.[2] It follows from this demonstration that total price equals total value:
(3) ∑Pj = ∑Vj
and it follows from (1´) , (2´), and (3) that
(4) ∑Cj + ∑Vj + ∑ πj = ∑Cj + ∑Vj + ∑Sj
which in turn implies that total profit equals total surplus-value:
(5) ∑ πj = ∑Sj
Finally, the “price” rate of profit is profit divided by invested capital, while the “value” rate of profit is surplus-value divided by invested capital. Since the denominators are the same, it follows from Equation (5) that the aggregate “price” and “value” rates of profit are also equal. ■
When deriving this result,[3] I imposed no special-case restrictions. Thus, the aggregate value-price equalities follow inevitably—without exception—from Marx’s account of the value-price transformation (as understood by the TSSI) and his demonstration in chapter 5 of Capital, volume 1. No special cases whatsoever can yield a contrary result.
Let me emphasize that I am not saying or implying that nothing can yield a contrary result. In principle, it would be possible to overturn the aggregate value-price equalities by disproving Marx’s demonstration in chapter 5 of Capital, volume 1. But no one has succeeded in disproving it.[4] Bortkiewicz did not even try, nor does Rallo.
3. The Aggregate Equalities in the Bortkiewicz-Rallo Special Case
Instead, Rallo continues to imagine, wrongly, that he can impose a restriction that creates a special case in which Marx’s aggregate value-price equalities are not preserved. To show that this is impossible—even more clearly than I showed it above—let us consider the special case that Rallo puts forward. It is actually an example constructed by Bortkiewicz that Rallo has raised from the dead.
As he stresses, the example satisfies the restriction that Rallo wishes to impose, which he very misleadingly calls “dynamic equilibrium”:
Dynamic equilibrium (absence of incentives, within the structure of prices of production itself, to modify the relations of production that have generated that structure of prices of production).
There is nothing dynamic about this kind of equilibrium. It is commonly called “static equilibrium.” I will therefore refer to it as “dynamic,” i.e., static (DIES). The acronym is fitting, since the equilibrium in question is the motionless equilibrium of a dead body, eternally at rest.
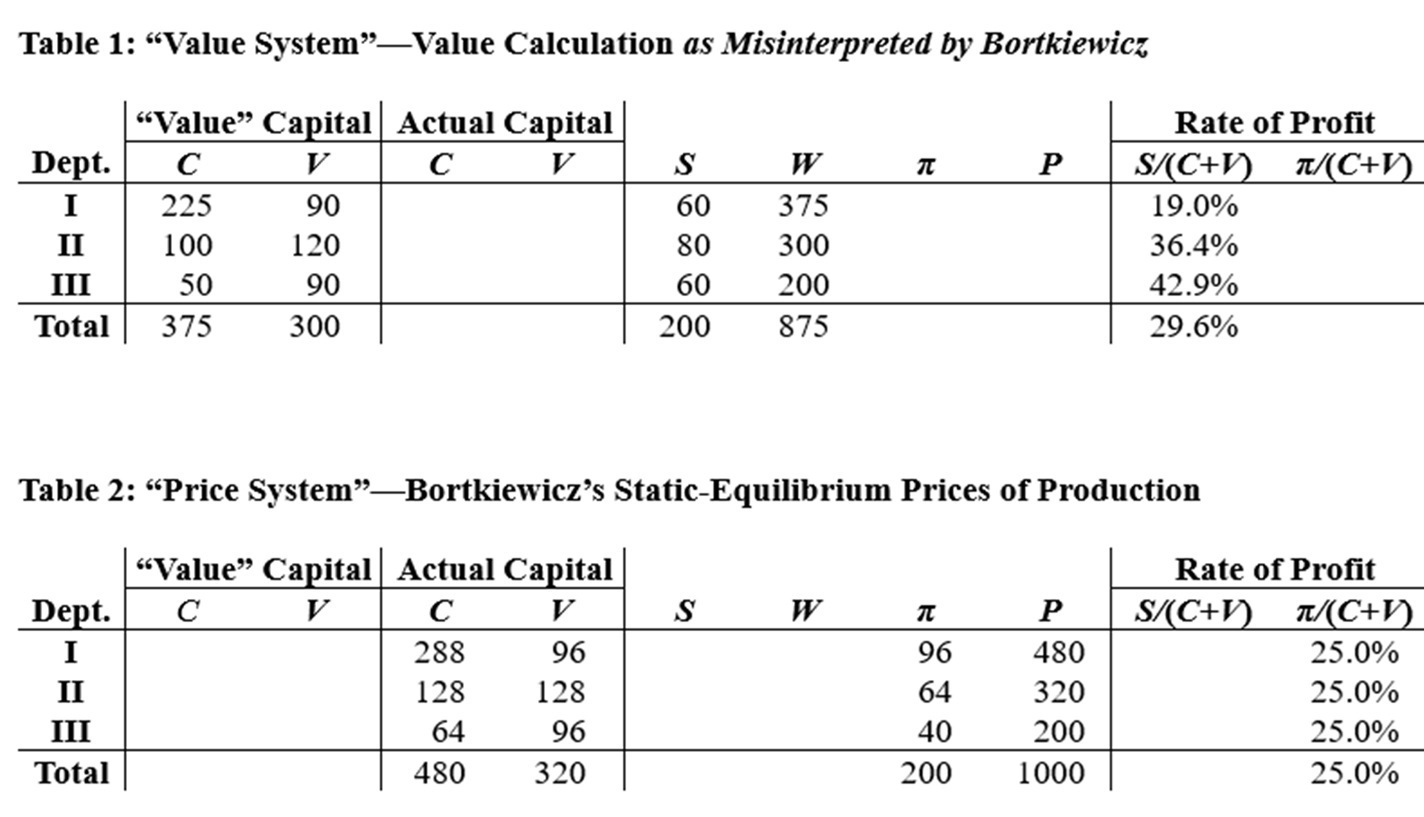
All figures in Tables 1 and 2, below, are taken directly from page 204 of Bortkiewicz’s “Correction,” except that I have also computed the rates of profit, which are not reported in his tables. The economy consists of three departments. Department I produces means of production, the material elements of constant capital, C. Department II produces workers’ means of subsistence, which investment of variable capital, V, funds indirectly. Department III produces luxury goods and services that are purchased using surplus-value, S, or profit, π.
Table 1 is the “value system” with which Bortkiewicz begins. He assumes that (a) commodities exchange at their values and (implicitly) that (b) per-unit values are stationary—the values of inputs (means of production and subsistence) equal the values of the outputs produced later in the same period. Bortkiewicz also assumes that (c) the “value system’s” economy is in a state of simple reproduction (notwithstanding Rallo’s efforts to evade this fact): “Finally, we shall assume ‘simple reproduction’” (Bortkiewicz, p. 200). Taken together, the three assumptions imply that the value of output of Department I must equal total C; that the value of output of Department II must equal total V; and that the value of output of Department III must equal total S.
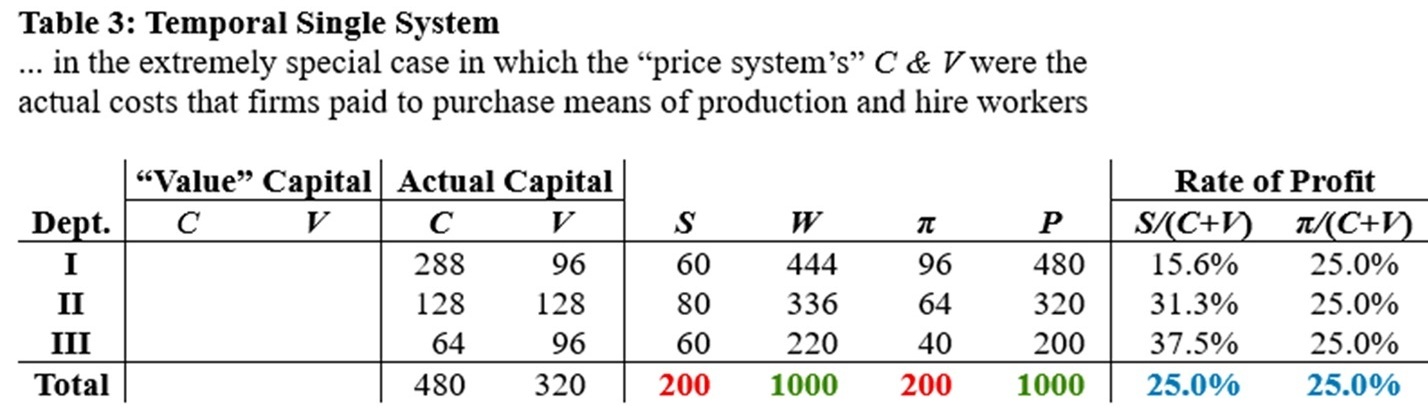
Bortkiewicz then converts this “value system” into the “price system of his Table 2. Now, the commodities do not exchange at their values. Instead, Bortkiewicz assumes that (a´) commodities exchange at their prices of production, which results in a uniform rate of profit throughout the economy. Also, he assumes (implicitly) that (b´) the prices of production are stationary. Finally, Bortkiewicz assumes that (c´) the economy is in the same state of simple reproduction as before, despite the shift from the “value system” to the “price system.” Taken together, the three assumptions imply that the price of output of Department I must equal total C; that the price of output of Department II must equal total V; and that the price of output of Department III must equal total π.
The economy of Table 2’s “price system” satisfies Rallo’s DIES equilibrium restriction, and it (or some multiple of it) is the only economy that does so.[5]
But what are the values of output and surplus-values of Table 2’s economy? Does the total price of output equal the total value? Does total profit equal total surplus-value? Let us see.
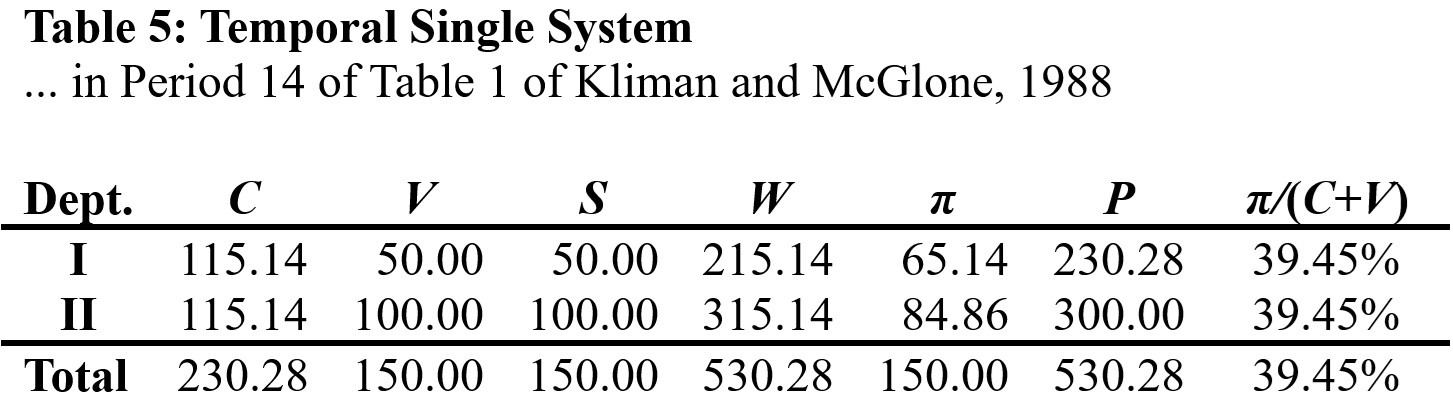
• It follows from Marx’s demonstration in Chapter 5 of Capital, volume 1, that total price equals total value (Equation (3)). Since the total price of output equals 1000, it must be the case that the total value of output equals 1000 as well. (See Table 3, which repeats the information in Table 2 and supplements it.)
• Furthermore, the C and V figures of Table 2 are (we are told by Bortkiewicz and Rallo) the actual costs that the firms in the “price system” economy pay to buy means of production and hire workers. According to the TSSI, Marx’s theory says that surplus-value is the difference between total value and these actual costs (this follows immediately from Equation (1)). So, since total C equals 480 and total V equals 320, it must be the case that total surplus-value equals 1000 – 480 – 320 = 200. Hence, total profit equals total surplus-value (Equation (5)).
• Finally, it follows immediately from this last equality that π/(C + V) = S/(C + V)—the aggregate “price” rate of profit equals the aggregate “value” rate of profit, which is 25% in this case.
(The surplus-value and value of output figures in each department are determined in the following manner. Bortkiewicz assumed (on p. 200, between his Equations (3) and (4)) that the rate of surplus-value, S/V, in each department is equal to the economy-wide rate. In the present case, that rate is 200/320. Thus, in each department, S = (200/320) × V. And when we add S to the department’s C and V, we obtain the total value of its output.)
Thus, as Table 3 shows, Marx’s aggregate value-price equalities are preserved—when his theory is interpreted in accordance with the TSSI—even in an economy that satisfies Rallo’s DIES-equilibrium restriction.
4. A Clarification, to Forestall Misinterpretation by Modelheads
Modelheaded economists, and other modelheads, will instinctively be driven to construe Table 3 as “the TSSI solution to the transformation problem.” That is completely wrong. In the first place, there is no transformation “problem”—no error in Marx’s account of the value-price transformation that needs to be corrected.
Secondly, Table 3 is not a model of the economy. There is no TSSI model. The TSSI is completely general; unlike models, it does not rely on any restrictive assumptions. There is thus no unique TSSI “solution”; the “solution” in any period depends crucially on the actual costs, C and V, of that particular period, and thus on the actual input prices of the particular period. When they change, so does the correct “solution.”
Table 3 simply depicts one, extremely special, case. Because of the special-case assumptions it makes, the Table 3 economy satisfies Rallo’s DIES-equilibrium restriction.
Specifically, Table 3 assumes that commodities exchange at their prices of production, that these prices are stationary, and that the economy is in a state of simple reproduction. But the TSSI itself does not require, and does not impose, any of these assumptions. Using (only) the data that Marx used in his account of the transformation—capital investments, components of cost prices, and surplus-values—it is able to compute the values of outputs, their prices of production, average profits, and the “value” and average “price” rates of profit. It is always able to compute them, whether or not the special-case assumptions of Table 3 happen to hold true. The computations always lead to the conclusion that the aggregate value-price equalities are preserved.
For instance, in an economy in which the physical inputs and outputs are identical to those of Table 3, but the prices are different, we might have the following case, in which commodities’ actual prices differ from their prices of production, prices are non-stationary, and the economy will not sustain a state of simple reproduction (see Table 4).
The C, V, and S figures are data (given). Everything in the next five columns is computed on the basis of these data. The figures in the final column are arbitrary; the point of this column is just to make clear that the actual prices differ from the prices of production.
Once again, all of Marx’s aggregate value-price equalities are preserved.
But if none of the special-case assumptions of Table 3 are either necessary or relevant to the matter at hand—the compatibility of Marx’s value theory and the real-world facts—why did I make these assumptions above, when presenting the transformation of values into prices of production?
I did so simply and solely to disprove Rallo’s claim that the TSSI and the aggregate value-prices equalities are incompatible with the DIES-equilibrium restriction he imposes.
The DIES equilibrium is just like a stopped clock that is right twice a day. The clock tells us that the current time is 11:42 and 17 seconds, which is wrong 99.998% of the time. A properly functioning clock almost never tells us that the current time is 11:42 and 17 seconds. But since it is a properly functioning clock, it has to be compatible with the case in which the current time really is 11:42 and 17 seconds. It can’t skip that one second; it has to function properly at every moment, without exception. So it has to tell us that the current time is 11:42 and 17 seconds in the extremely special case in which that happens to be right—when (but only when) the immediately preceding time was 11:42 and 16 seconds.
In the same way, the prices of production of Marx’s theory are almost never DIES-equilibrium prices. But since it is a properly functioning theory, Marx’s theory has to be compatible with DIES equilibrium—and we have seen that it is. It can’t skip that one case; it has to function properly in all cases, without exception. So it has to say that prices of production are DIES-equilibrium prices in the extremely special, and completely hypothetical, case in which that happens to be right—when (but only when) the C and V of the Bortkiewiczian “price system” happen to be the actual amounts of money invested as constant and variable capital, because commodities’ actual prices happen to be both stationary and prices of production.
5. The Temporal Single-System Interpretation is a Single-System Interpretation
We have seen that, when Marx’s theory is interpreted in accordance with the TSSI, all of his aggregate value-price equalities are preserved, even in an economy that satisfies Rallo’s DIES-equilibrium restriction. This result is the exact opposite of what Rallo claims in his reply to me:
when both inputs and outputs are exchanged at their prices of production, the double aggregate equality (value-prices of production; surplus value-profit) does not hold. This is, in fact, Bortkiewicz’s criticism of the transformation problem that the TSSI attempts to overcome, without success.
Rallo is completely wrong about this, as we have seen. But why does he say something so completely false?
The reason is that he continues not to understand that the temporal single-system interpretation is a single-system interpretation. He therefore fails to ask whether the price and profit of the single system (Table 3) are equal to the value and surplus-value of the single system.
Instead, he compares the price and profit figures of Bortkiewicz’s “price system” (Table 2) to the value and surplus-value figures of Bortkiewicz’s separate “value system” (Table 1). That comparison is completely irrelevant and illegitimate here. As a single-system interpretation, the TSSI rejects the “value system” in its entirety. It denies that the constant and variable capital figures of the “value system” are those of Marx’s theory, and it therefore also denies that the surplus-value and value figures of the “value system” are those of Marx’s theory. The figures for these variables that conform to Marx’s theory—in the extremely special DIES-equilibrium case we have considered—are instead those of Table 3’s single system.
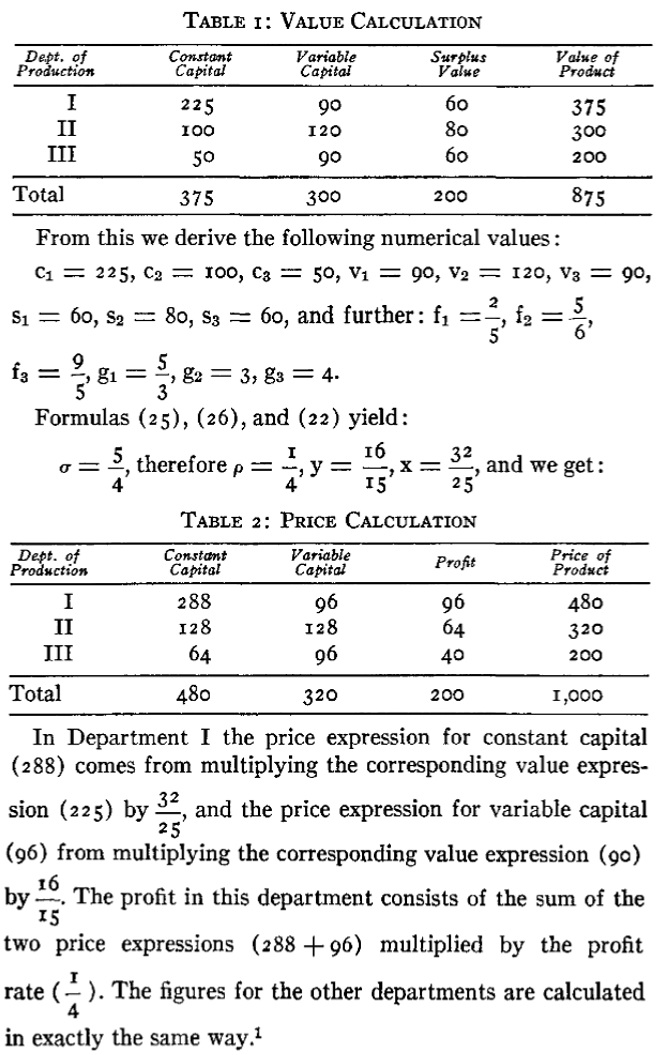
Let me note that this is not the first time that Rallo is seeing the TSSI in the context of an example that satisfies his DIES-equilibrium restriction. In Anti-Marx, he cites Kliman and McGlone (1988). In Table 1 (p. 73) of that paper, Period 14 is a DIES equilibrium. The relevant figures (using the notation of the present article) are:
Rates of profit are equal. The economy is in a state of simple reproduction. Prices are stationary. Supplies of both goods equal the demands for them.[6] But here again, according to the TSSI, total price equals total value, total profit equals total surplus-value, and the aggregate “price” and “value” rates of profit are equal.
In my critique of Rallo’s book, I mentioned that “[i]t is unclear to me whether Rallo fully understands that the TSSI is a single-system interpretation rather than an iterative ‘solution’ to the alleged transformation problem. His discussion of this matter (vol. 1, section 5.2) is quite ambiguous” (endnote 10). I therefore took pains to explain the difference:
In contrast to single-system interpretations, but like other dual-system “solutions,” iterative “solutions” wrongly take the term “value of constant capital” to mean the value of the means of production and wrongly take the term “value of variable capital” to mean the value of the means of subsistence (wage goods). … The TSSI does not do so. … The TSSI itself does not conflate the value of invested capital with the value of its material elements ….
In section 4 of the same article, I wrote
the data that Marx employed in his computations are enormously different from the data with which Bortkiewicz and all other simultaneist theorists begin. …
To compute [Marx’s prices of production], we only need to know the period’s capital investments, components of cost prices, and surplus-values. We do not need to know the input-output relations, physical quantities, or input prices. …
In short, Marx’s procedure is entirely general. It does not rely on any restrictive assumptions whatever.
I also wrote, in Section 6, that
neither Marx nor the TSSI conceive of the formation of prices of production as a shift from a system of exchanges at values to a system of exchanges at prices of production. They do not start from exchanges at values, nor do they conflate the formation of prices of production with exchanges at prices of production. Given this alternative conception, Marx’s account as well as the TSSI’s defense of it are perfectly “consistent with the economic conditions that would allow the simple reproduction of capital,” even when inputs are substitutable and firms maximize profits.
Rallo is clearly aware of what I wrote. Indeed, he quotes the first sentence-and-a-half of the Section 6 passage in his reply to me. Yet what does he do? He starts from a system of exchanges at values (Table 1). Then he shifts to a system of exchanges at prices of production (Table 2). Then he declares that the totals don’t match. Finally, he triumphantly blames the discrepancies on Marx and the TSSI!
What he should have blamed, instead, is his own failure to understand that the TSSI is a single-system interpretation.
In my critique of Anti-Marx, I was very reluctant to draw the conclusion that Rallo failed to understand this. After all, he seems to have read a good deal of TSSI work, he criticized it extensively, and he is so confident of his command of the issues that he represents his work as the “titanic … destr[uction of] Marx’s economic thought.” Could it really be the case that he misunderstands the TSSI so egregiously? So I wrote, more tentatively, that “[i]t is unclear to me whether Rallo fully understands that the TSSI is a single-system interpretation.” But now that his reply to me has uncomprehendingly repeated his misinterpretations, even after all my efforts to explain that the temporal single-system interpretation is a single-system interpretation, I have to conclude that he has not understood this.
6. Rhetoric Replaces Logic: Rallo’s “Excuses” and “Very Exceptional Assumptions”
I have already made it crystal-clear that there are absolutely no cases in which the TSSI fails to preserve Marx’s aggregate value-price equalities. But let me make it even clearer by considering Rallo’s claim that I put forward the “excuse” that “the TSSI is compatible with [simple reproduction] under very exceptional assumptions.”
I made no such excuse since, to repeat myself once more, no excuse is necessary: the TSSI preserves the aggregate equalities in all cases, without exception. And Rallo’s “very exceptional assumptions” line just throws out logic and replaces it with overheated rhetoric.
What are the “very exceptional assumptions” to which he refers? First, there is the case in which “capitalists do not seek to maximize profits, or substitutability between means of production and labor is not possible.” Second, “the TSSI would be compatible with … simple reproduction when ‘exchanges take place at prices that differ from prices of production.’” And finally, the “[t]hird exceptional case: when both inputs and outputs are exchanged at their prices of production.”
What Rallo’s rhetoric obscures is the fact that, taken together, these three “very exceptional” cases include all cases, without exception (see Figure 1). The “excuse” I put forward was that Marx’s theory and the TSSI are compatible with simple reproduction whether or not commodities exchange at their prices of production, and whether or not firms are profit maximizers that can engage in input substitution. And that exhausts the universe of cases. Every case is one in which commodities either do or do not exchange at their prices of production and firms either are or are not profit maximizers that can engage in input substitution.
Figure 1
In his reply to me, Rallo tacitly acknowledges that I am right about the first two cases. As for the third, he claims that “when both inputs and outputs are exchanged at their prices of production, the double aggregate equality (value-prices of production; surplus value-profit) does not hold.” We have seen that this claim is false; the double aggregate equality does hold, because the TSSI is a single-system interpretation, not the dual-system interpretation Rallo imagines it to be. So I am right about all three cases—that is, right about all cases.
But perhaps Rallo can conjure up some case in which the TSSI isn’t compatible with simple reproduction. How about a case of beer? A briefcase? A quesadilla? Karl Case? Case Western Reserve University?

7. The Law of Value and the Rate of Profit: Misrepresenting, Having it Both Ways, Failing to Respond
In his Anti-Marx, Rallo argued, correctly, that if firms are profit maximizers and inputs are substitutable, it is generally impossible for the economy to be in the same state of simple reproduction at two different sets of prices. Thus, an economy in which commodities exchange at their values cannot be in the same state of reproduction as an economy in which the commodities exchange at their prices of production.
In my critique of the book, I pointed out that this means that every “solution” to the “transformation problem” that requires preservation of the initial state of simple reproduction is wrong: (a) every existing and potential simultaneist “solution,” and (b) Marx’s account and the TSSI’s defense of it—as misinterpreted by Bortkiewicz, Rallo, etc.:
Rallo’s own argumentation leads to the conclusion that the simultaneist “solutions” violate simple reproduction. …
Thus, it also follows from Rallo’s argument that, if one rejects any “solution” that is incompatible with simple reproduction, one must reject not only Marx’s account and the TSSI’s defense of it, but also Bortkiewicz’s “correction” as well as every existing and potential simultaneist “solution.” (As I will discuss below, both Marx’s account and the TSSI defense are actually compatible with simple reproduction, but only when they aren’t misinterpreted in the manner of Bortkiewicz, Rallo, and adherents of dual-system interpretations generally.) [Emphasis in original.]
Rallo egregiously misrepresents this statement. He claims that it is another “excuse,” and he bizarrely charges me with having said that the TSSI must be right because Bortkiewicz was wrong:
Does the fact that Bortkiewicz could be wrong imply that the TSSI must be right? Obviously not. From the fact that Bortkiewicz could fail to posit a coherent transformation of values into prices of production, it does not follow that the TSSI has arrived at a correct solution.
But I did not say or imply that the TSSI must be right because Bortkiewicz was wrong. On the contrary, I said that if the (misinterpreted version of the) TSSI is wrong, then so are all simultaneist “solutions,” and vice-versa. And therefore, I said, logical consistency demands that, if you reject one because it is incompatible with simple reproduction, you must also reject the other.
I was warning Rallo that he can’t have it both ways.
I returned to this issue at a later point in my critique, when I demolished his book’s attempt to prove that the law of value doesn’t determine the real rate of profit, that is, the “price” rate. His “proof” was that the rate of profit of a Bortkiewiczian “price system” can change even though the rate of profit of its “value system” does not.
Rallo was (inadvertently) having it both ways here. On the one hand, his Anti-Marx rejects Marx’s theory because—after Rallo imposes his additional restrictions—it doesn’t preserve the same state of simple reproduction at two different sets of prices. On the other hand, Anti-Marx accepts Bortkiewicz’s “correction” of Marx even though that “correction” also fails to preserve the same state of simple reproduction at two different sets of prices. Indeed, it uses the “correction” to try to prove that the law of value doesn’t determine the “price” rate of profit.
Rallo’s attempted proof is a failure, and not only because it has it both ways. In addition, by failing to recognize that Bortkiewicz’s “correction” disrupts simple reproduction, its logic and economics are a mess. As I pointed out,
the general rates of profit in Bortkiewicz’s “price system” and in Rallo’s modified version of it are bogus. These rates of profit presuppose that all departments are able to sell everything they produce, but that is not the case, since the disruption of simple reproduction causes demand for some goods to fall short of supply. So Rallo’s demonstration that two bogosities are unequal to one another although the “value system’s” rate of profit remains unchanged is rather meaningless.
In his reply to me, Rallo refrains from commenting directly on this demolition of his attempted refutation of the law of value.
8. Having it Both Ways 2.0
But he has not learned his lesson. Far from it. Even after I warned Rallo that he can’t have it both ways, his reply to me is an exercise in have-it-both-ways argumentation.
The whole thing reduces to the following: Once Rallo imposes his restrictions that firms maximize profits and inputs are substitutable, the economy cannot be in the same state of simple reproduction at two different sets of prices. In his misinterpretation of Marx’s account of the transformation of values into prices of production, there are two different sets of prices (the “value system’s” values and Marx’s prices of production), so the economy cannot be in the same state of simple reproduction in both cases. Hence, Rallo maintains, Marx and the TSSI derive the aggregate value-price equalities in an unacceptable way.
Furthermore, Bortkiewicz’s dual system does not preserve the aggregate equalities. And that dual system is the correct solution, according to Rallo—even though it contains two different sets of prices (the “value system’s” values and the “price system’s” prices of production), so that the economy cannot be in the same state of simple reproduction in both cases.
Hence, Rallo concludes, Marx’s aggregate value-price price equalities do not hold true … because it is totally unacceptable that Marx and the TSSI fail to ensure the same state of simple reproduction at two different sets of prices, but it is completely fine and dandy that Bortkiewicz and Rallo fail to ensure the same state of simple reproduction at two different sets of prices.
Rallo does not put it this way, of course. Instead, he tries to justify his have-it-both-ways argumentation by telling us a blatantly false story about the relation between Bortkiewicz’s “value system” and his “price system.”
9. Rallo’s Falsification of Bortkiewicz’s “Correction” of Marx
Rallo objects to the following statement I made in my critique of his Anti-Marx: “When (mis)conceived as Bortkiewicz, Rallo, et al. conceive it, the transformation of values into prices of production is a shift from a system in which goods exchange at their values to a system in which they exchange at their prices of production.” According to Rallo, I am mistaken about the direction in which Bortkiewicz proceeded:
The mistake Kliman makes is to think that Bortkiewicz’s set of values (Table I) represents a situation of economic equilibrium in which exchanges are made (in conditions of static equilibrium) that structure production relations (in dynamic equilibrium) and that, subsequently, this scheme of values is transformed into a set of prices of production (Table II or Table III), which, by altering the relative prices of the inputs (with respect to those in Table I), will necessarily modify the original structure of production ….
In sum, for Bortkiewicz there is no productive structure α derived from the value system that, consequently, must be transformed into a productive structure β when the value system is transformed into the system of prices of production: there is a single productive structure derived from the system of prices of production that can be expressed/represented/computed in terms of values (of hours of social labor). [Emphases added.][7]
And what is the textual evidence that Rallo provides, about what Bortkiewicz did first, what he did second, and what he derived from what? He provides no textual evidence whatsoever—no quotations, no paraphrases, no page citations, nada. Rallo’s whole story about how Bortkiewicz proceeded is just made up.
He tells us that his story must be right, not because the textual evidence indicates that it is right, but because the alternative (as Rallo misunderstands it) is “unthinkable.” It is not the way capitalism works. Capitalists try to maximize profit, but the capitalists of Table 1 do not.
If the question were “How would Bortkiewicz have proceeded if he thought like Rallo and if he were trying to produce a model of how capitalism works?,” this would be a great answer. It is no answer at all to the actual question here: “How did Bortkiewicz actually proceed, in a context in which he was trying to prove that Marx’s transformation procedure was wrong and trying to correct that procedure?” Rallo has lost sight of the difference between a model and an attempted proof, and between a presentation of one’s own view and an attempt to disprove one’s opponent. Or, perhaps, he just wants his readers to lose sight of the differences.
To discover how Bortkiewicz actually proceeded, we have set aside the issue of what is unthinkable to Rallo and turn instead to the textual evidence.
(1) The text of Bortkiewicz’s “correction” begins on page 199. He writes there that Tugan-Baranowsky’s correction of Marx starts with prices of production and the average rate of profit and uses them to derive values and the rate of surplus-value. Bortkiewicz says that this is “the opposite of [the problem] which Marx tried to solve,” and that he will “show that Marx erred … without reversing his way of posing the problem.” In other words, he will start with values and surplus-values and derive prices and profit from them, since that was Marx’s way of posing the problem.
(2) On pages 199-200, Bortkiewicz states three “limiting assumptions” he will make. The final one is “we shall assume ‘simple reproduction’” (see Figure 2). Since he says nothing more, to restrict the scope of the assumption, this means that he assumes simple reproduction throughout. So the economy is assumed to be in a state of simple reproduction from the start, when he constructs his “value system.”
Figure 2
(3) Bortkiewicz then presents the “value system” in Equations (1) through (3), also on page 200. He says explicitly that these equations satisfy “[t]he conditions of simple reproduction” (see Figure 2).
(4) On page 201, Bortkiewicz writes that “the problem now is to convert these value expressions into price expressions.” He argues that Marx did so improperly, after which he starts to present his own “correct transition from value quantities to price quantities.” The direction in which he is proceeding is obvious.
(5) On page 202, Bortkiewicz’s writes down his prices of production, Equations (11) through (13). These equations make use of the relations of simple reproduction of his “value system,” without altering them. That is, the total value of output of Department I is expressed as the sum of the values of constant capital of all three departments, and the equations for the other two departments are analogous.
Equations (11) through (13) convert these “value” magnitudes into “price” magnitudes by multiplying each “value” magnitude by the relevant department’s price/value ratio. This is equivalent to taking the total value of each physical quantity, dividing by the value per unit to obtain the physical quantity, and then multiplying the physical quantity by the price per unit to obtain the total price of the physical quantity. In other words, it is equivalent to keeping all physical quantities unchanged but revaluing them.
Thus, in Bortkiewicz’s “correct transition from value quantities to price quantities,” all physical quantities are those of his value system, and all of them remain unchanged in the “transition.” Since the system of physical quantities was in a state of simple reproduction before the “transition,” it follows that it remains in that same state of simple reproduction thereafter. The only things that have changed are the exchange ratios; Bortkiewicz has shifted from a system in which goods exchange at their values to a system in which they exchange at their prices of production.
(6) After discussing his choice of numéraire and solving his price-of-production equations, Bortkiewicz provides (on pp. 204-205) a numerical example of his procedure and its results, our beloved Tables 1 and 2 (see Figure 3). In the text following each table, Bortkiewicz reiterates what we have already learned about his procedure, including the direction in which he proceeded.
Figure 3
He says that he took the value magnitudes of Table 1 and plugged them into his formulas (25), (26), and (22) to obtain four ratios. One ratio is y = 16/15, the price/value ratio of Department II’s product. Another is x = 32/25, the price/value ratio of Department I’s product. Bortkiewicz then says that his price expressions were obtained by multiplying the associated value expressions by these price/value ratios. As I noted above, this is equivalent to leaving all physical quantities of the “value system” unchanged—and, thus, leaving the “value system’s” state of simple reproduction unchanged—but revaluing each physical quantity at its price of production instead of at its value.
Rallo’s claim, that “for Bortkiewicz there is no productive structure α derived from the value system … there is a single productive structure derived from the system of prices of production,” is therefore a fabrication that flatly contradicts the textual evidence. As we have seen, Bortkiewicz deduced the productive structure from his “value system,” and he assumed that this productive structure is preserved in the “price system,” even though prices change.[8]
10. The Sinking of the Titanic Destruction of Marx’s Economic Thought
Now that the record has been set straight—Bortkiewicz’s procedure is a “transition from value quantities to price quantities” (p. 201), not vice-versa—we are back where we started when I first warned Rallo about his have-it-both-ways argumentation. Its logic and economics are a mess.
Once he imposes his profit-maximization and-input substitution restrictions, in an attempt to refute Marx and the TSSI (as he misunderstands them), he has an economy that would be in a state of simple reproduction if commodities exchanged at their values, but this economy cannot be in the same state of simple reproduction if commodities instead exchange at prices of production. So simple reproduction is disrupted in the “transition from value quantities to price quantities.” The change in prices induces input substitution, which in turn causes demand for some goods to fall short of supply, which in turn reduces the rates of profit of industries that produce these goods.
Hence, the “price system’s” rates of profit, which need to be equal, are not equal. But its prices are prices of production if and only if all rates of profit are equal (this is true by definition). Thus, the prices of the “price system” are not actually prices of production. In short, the figures in the “price system” table are bogus. So, while Marx’s aggregate value-price equalities are not preserved, this doesn’t disprove the law of value. Marx certainly did not contend that total value equals bogus total price, or that total surplus-value equals bogus total profit, or that the aggregate “value” rate of profit equals the aggregate bogus “price” rate of profit.[9]
* * *
But let’s imagine, for the sake of argument, that Bortkiewicz’s procedure were the “transition from price quantities to value quantities” that Rallo tells us it is. What would we then have? The same thing that we had before: a change in prices that induces input substitution, disequilibrium between supplies and demands, and disruption of simple reproduction. As a result, the economy of the “value system” is physically different from the economy of the “price system.”
So, while Marx’s aggregate value-price equalities are not preserved, this doesn’t disprove the law of value. Marx certainly did not contend that the total price of output in Poland equals the total value of output in Russia, or that total profit received in Ireland equals total surplus-value generated in China; or that the “price” rate of profit in Belgium equals the “value” rate of profit in the US. He was referring to the price and value aggregates of one and the same economy, not to the aggregates of two physically different economies.
But—I anticipate Rallo objecting—the “transition from price quantities to value quantities” is not a real transition. There is only one actual economy, the “price system,” so there is only one physical structure, that of the “price system.” The “value system” is just the result of a thought experiment in which we ask, “if goods were to exchange at their values instead of their prices of production, how would that change things?” In fact, this may be what Rallo meant when he wrote that “Table I is not a temporal antecedent of Table II or Table III; it is a logical antecedent …. [T]here is a single productive structure derived from the system of prices of production that can be expressed/represented/computed in terms of values.”
This excuse (if I may speak Ralloese) doesn’t work at all. The thought experiment violates the input-substitution restriction that Rallo himself has imposed.[10] If inputs are substitutable, there is not “a single productive structure derived from the system of prices of production.” The imaginary switch from exchange at prices of production to exchange at values will induce profit-maximizing firms to engage in imaginary input substitution, which will lead to an imaginary disruption of the “price system’s” state of simple reproduction. So what we end up with is not only two different systems of exchange (one actual, one imaginary), but also two physically different economies (one actual, one imaginary). Comparing their aggregates would be like comparing actual apples and imaginary oranges.
But—I anticipate Rallo objecting again—input substitution will not take place in the imaginary “transition from price quantities to value quantities” because the capitalists of the imaginary “value system” are not profit maximizers. (There is a hint of this gambit in his reply to me: “if the capitalists exchanged according to the set of values in Table I, the capitalists would not be seeking to maximize profits.”) Fine. Let us assume instead that the “value system’s” capitalists are square-number maximizers. Their objective function is to maximize the number of components of the total value of their products that are square numbers, given their technology and the prevailing input prices (values), and subject to the constraint that there are three components of total value, C, V, and S. So, instead of Bortkiewicz’s Table 1, we might have Table 6, below. The capitalists have succeeded in optimizing subject to constraint: all three components of total value in all three departments are square numbers.
Here, again, we have an economy that is physically different from Table 2’s “price system.”[11] So, while Marx’s aggregate value-price equalities are not preserved, this doesn’t disprove the law of value, because comparison of the aggregates of two physically different economies continues to be an apples-to-oranges comparison.
To put the point here in general terms, if the capitalists of the imaginary “value system” are not profit maximizers, they will seek to maximize something else, or to minimize something, or they will satisfice, or they will settle for just flailing around. They have no incentive, in any of these cases, to maintain the “price system’s” state of simple reproduction. So the end result will be two physically different economies whose aggregates cannot be meaningfully compared.
* * *
Rallo dug himself into a hole. He can’t get out of it.
In an attempt to overturn Marx’s aggregate value-price equalities, he appealed to Bortkiewicz’s “correction” of Marx, which claims that the equalities do not hold true. But this didn’t work, because the TSSI shows that no correction of Marx is needed. It preserves his equalities, and it does so without violating Bortkiewicz’s restriction that simple reproduction must also be preserved.
So Rallo piled on additional restrictions: inputs must be substitutable and capitalists must maximize profits.
In general, it is impossible to satisfy the whole set of restrictions, because input substitution is incompatible with simple reproduction. Any change in relative prices will induce profit-maximizing firms to engage in input substitution in order to reduce costs, but input substitution will disrupt simple reproduction. The whole set of restrictions can be satisfied in one case only: the case in which relative prices are stationary. Rallo himself has said this repeatedly.
The TSSI is able to satisfy the whole set of restrictions—and still preserve the equalities—because it is compatible with stationary prices, as I have shown here.
But simultaneist “solutions” to the alleged transformation problem, including Bortkiewicz’s “correction,” cannot satisfy the whole set of restrictions. The reason they cannot is that, as they (mis)understand the transformation of values into prices of production, it is precisely a change in relative prices. It is either a shift from a system of exchange at values to a system of exchange at prices of production or the reverse shift that Rallo has now proposed. In either case, the change in prices induces input substitution, which in turn disrupts simple reproduction.
These “solutions” say that Marx’s aggregate equalities do not hold true. But Rallo must reject these “solutions” and what they say about the aggregate equalities, because they cannot satisfy his whole set of restrictions.
In sum, the aggregate equalities emerge unscathed. This result is diametrically opposed to the result that Rallo hoped to achieve by piling on his added restrictions.
This is the hole that he has dug himself into and that he can’t get out of. As we have seen, reversing the direction of the transition from one system of exchange to the other makes no difference. Treating the transition as a thought experiment doesn’t work without violating the input-substitution restriction. Getting rid of the profit-maximization restriction fails to eliminate the disruption of simple reproduction.
The root of the problem is that Rallo imposed the input-substitution restriction on top of the simple-reproduction one. He can’t have it both ways: in a transition from one set of relative prices to another, these two restrictions are just not compatible.
But perhaps Rallo can conjure up some case in which they are compatible? How about …


ENDNOTES
[1] I put “Marx” inside scare quotes here because it is actually Rallo’s version of Marx’s argument, which is a misinterpretation, that is incompatible with simple reproduction (given Rallo’s restrictions). As I discuss in the final subsection of this article, Marx’s actual account of the transformation is compatible with simple reproduction.
[2] If someone sells something for $x more than its value, someone else buys it for $x more than its value, and the buyer’s loss of –$x exactly offsets the seller’s gain: $x + (–$x) = 0. “The sum of the values in circulation can clearly not be augmented by any change in their distribution. … The capitalist class of a given country, taken as a whole, cannot defraud itself” (Marx, 1990, Capital: A Critique of Political Economy, vol. 1, pp. 265-266 (London: Penguin Books)). For further discussion of Marx’s demonstration in chapter 5, see my 2011 paper, “On Capitalism’s Historical Specificity and Price Determination: comments on the value-form paradigm.”
[3] Marx’s argument in chapter 9 of Capital, volume 3 proceeds in the opposite direction, starting from the equality of the “price” and “value” rates of profit and deducing the other two aggregate equalities from this one. I reversed the direction of the argument to simplify the exposition. This makes no difference in the end; once any of the equalities is established, the other two follow from it immediately.
[4] One unsuccessful refutation is the argument that the capitalist class receives profit in excess of surplus-value (and that total price therefore exceeds total value) because the capitalists defraud the workers. This argument fails, even if the workers are in fact defrauded. If d is the amount by which workers are defrauded, profit increases from πo to π1 = πo + d while wages and benefits fall from Vo to V1 = Vo – d. (This is true even if the fraud takes the form of overcharging workers in the market instead of underpaying them. If a worker who is paid Vo can now buy only Vo – d worth of stuff, his/her real wage has fallen to Vo – d even though his/her nominal wage is still Vo). But since V + S is equal to the new value created in production, N, and the new value remains constant, the fall in wages and benefits causes surplus-value to rise from So to S1 = So + d. (Since So = N – Vo, S1 = N – V1, and V1 = Vo – d, it follows that S1 = N – V1 = N – (Vo – d) = (N – Vo) + d = So + d.) Thus, S and π rise by the same amount, d; the capitalist class does not receive profit in excess of surplus-value.
[5] By “multiple” of the Table 2 “price system,” I mean an economy in which every C, V, π, and P is a constant multiple of its Table 2 counterpart, such as an economy in which all C, V, π, and P figures are double those, or half of those, in Table 2.
[6] Department I supplies means of production, which are priced at 230.28. The demand for means of production, total C, is also 230.28. Department II supplies all articles of consumption. Their total price is 300. Total demand for articles of consumption is also 300, since it is the sum of the amount that workers demand (equal to total V) and the amount that capitalists demand (equal to total π).
[7] What Rallo means by “structure of production” and “productive structure” is a system of physical quantities of inputs (including workers’ means of subsistence) and outputs.
[8] Rallo’s reply contains a second distortion of Bortkiewicz’s procedure as well. He writes that “Table I is … a representation, in terms of values (of hours of social labor), of the relations of production contained in Tables II or III …. [T]here is a single productive structure derived from the system of prices of production that can be expressed/represented/computed in terms of values (of hours of social labor).” The prose here is somewhat vague, but Rallo certainly says that Bortkiewicz expressed value in terms of units of labor-time, not in terms of units of money values. That is not true. On page 202, Bortkiewicz wrote that he was assuming that “the price unit and the value unit are … identical,” and that gold “serves as the value and price unit.” In other words, both the value figures in Table 1 and the price figures in Table 2 are amounts of gold. (For example, in Department II, the amount of money invested as constant capital is 100 ounces of gold in the “value system” but 128 ounces of gold in the “price system.”) Also, in a footnote on page 205, Bortkiewicz criticized Tugan-Baranowsky, who “sets up his schema in terms of labor units instead of money units. This is legitimate enough, but it turns attention away from the real difference between value calculation and price calculation.”
[9] This and the preceding paragraph are exclusively about the implications of Bortkiewicz’s “correction” after Rallo’s additional restrictions are imposed on it. I am well aware that Bortkiewicz himself did not stipulate that inputs are substitutable, and that dual-system models fail to preserve Marx’s aggregate equalities whether or not simple reproduction is assumed, and that none of this has anything to do with Marx or the TSSI, because the “value system” has nothing to do with Marx or the TSSI.
[10] Of course, Bortkiewicz’s original “transition from value quantities to price quantities” is no less imaginary than Rallo’s inverse procedure. So if it’s fine and dandy to ignore the input-substitution restriction in imaginary cases, it’s fine and dandy for TSSI theorists to ignore it when showing that—pace Bortkiewicz—Marx’s transformation procedure obtains his aggregate equalities without disrupting simple reproduction. Thus, we have yet another reason why Rallo needs to retract his charge that the TSSI is “inconsistent with the economic conditions that would allow the simple reproduction of capital” (Anti-Marx, Vol. 2, section 5.4.1).
[11] If the economies were physically identical, then all C figures in Table 6 would differ from the C figures in Table 2 by the same percentage, and all V figures in Table 6 would differ from the V figures in Table 2 by the same percentage. That is not the case here.
Editor’s note, May 16, 2025: Endnote numbering has been corrected.
Editor’s note, May 17, 2025: Table 4 has been corrected.








Dear Professor Kliman,
The physicist and mathematician Álvaro Romaniega has raised a critique regarding this passage of yours:
*“Let me emphasize that I am not saying or implying that nothing can yield a contrary result. In principle, it would be possible to overturn the aggregate value-price equalities by disproving Marx’s demonstration in Chapter 5 of Capital, Volume 1. But no one has succeeded in disproving it.[4] Bortkiewicz did not even try, nor does Rallo.”*
Romaniega argues that in Rallo’s book—which you have not read in full—there is indeed an attempt to disprove Marx’s demonstration, exposing its alleged falsity and logical flaws. He further develops this argument in the following paper:
https://alvaroromaniega.wordpress.com/wp-content/uploads/2021/08/criticatvt2014.pdf
In essence, Romaniega’s thesis is that even if the TSSI were to salvage the coherence of Marx’s theory, it would still rest on false premises. Given today’s AI tools, translating his paper into English would be straightforward, and it would be interesting to see a response to it.
Additionally, I’m attaching this mathematical note, which addresses your latest reply to Rallo:
https://alvaroromaniega.wordpress.com/2025/04/28/nota-matematica-sobre-la-tssi-como-solucion-al-problema-de-la-transformacion-de-marx/
Best regards,
Hi Antonio! Glad to hear from you.
I just now saw your comment, but I noticed the same claim by Romaniega. Below is what I wrote to him, on June 8. I haven’t received a reply (yet). I’m not certain, but I suspect he has confused chapter 1 of Capital with chapter 5.
From: Andrew Kliman
Sent: Sunday, June 8, 2025 11:39 AM
To: alvaroromaniegadoc@gmail.com
Subject: Citation question, premises question
Dear Álvaro Romaniega,
In response to my statement that
In principle, it would be possible to overturn the aggregate value-price equalities by disproving Marx’s demonstration in chapter 5 of Capital, volume 1. But no one has succeeded in disproving it.[4] Bortkiewicz did not even try, nor does Rallo.
you recently wrote
Es evidentemente falso que nadie haya mostrado que la demostración de Marx es incorrecta. Sin ir más lejos, en mi trabajo [Rom20] analizo expresamente la demostración de Marx y expongo los errores lógicos que contiene. Y es evidentemente falso que Rallo no lo haya hecho, ver [Ral22, Capítulo 1, Volumen II].
I haven’t found the responses to Marx’s demonstration that you cite. Ral22, Capítulo 1, Volumen II is 260 pages long, and Rom20 is also not short. Could you please provide more specific citations, with page numbers? Please note that I’m asking specifically and only about Marx’s demonstration in chapter 5 of Capital, volume 1—in the Siglo Veintiuno Spanish edition, this is the second section of Capítulo IV, “Contradicciones de la formula general” (pages 190-202 of Tomo I/Vol. 1)—not his arguments in the 1st chapter.
Also, in response to my statement that “prices of production exist as the long-run average (average over time) of the actual (market) prices that fluctuate around them,” you recently wrote, “No existe demostración de tal afirmación.” I don’t know what this means. What sort of demonstration/proof do you want? What are its premises?
Hi Antonio and Andrew,
I have translated the whole text to ease communication, so everything should now be clearer. Sorry for the delay in responding — I had other issues to attend to first.
https://alvaroromaniega.wordpress.com/2025/04/28/nota-matematica-sobre-la-tssi-como-solucion-al-problema-de-la-transformacion-de-marx/
There’s no confusion: in my note I make the two steps of the proof explicit and keep them separate:
(1) surplus value is not generated in circulation, so $\sum_i \Delta p_i\,x_i = 0$;
(2) what commodities are “worth” ($p_i^{o}$) is given by their values ($\lambda_i$).
Both steps are spelled out in the new English and Spanish versions. For the specific claim $g_t \cdot x_{t+1}=0$, the essential content comes from Chapter 1; Chapter 5 is the more trivial exchange-accounting part—see the footnote for the formal pairing argument.
In any case, everything is stated rigorously in the note. If you can refer to the specific equation numbers and follow the same notation, we can advance the discussion more productively.