More False Claims from Moseley, and Still No Demonstrations

 
by Andrew Kliman, author of Reclaiming Marx’s “Capital”: A Refutation of the Myth of Inconsistency

 
Fred Moseley has replied to the second of my articles that have exposed his failure to demonstrate what he claims. (His comment is reprinted in full below.) What he writes in his reply is false, irrelevant, a return to his bait-and-switch stratagem, and a smokescreen that obscures the fact that he is unable to demonstrate his claims and unwilling to put them to the test.
 
 
The Irrelevant Matter

The falsity of Moseley’s reply is actually the least important of its failings. The reason it is not terribly important is that, in this case, his false claims are about an irrelevant matter. Moseley has decided to divert the debate onto the irrelevant question of whether, in Marx’s original theory, the rate of profit can change because there is a change in distribution of capital across sectors of the economy, even when technology and the real wage rate are unchanged. This is irrelevant to the debate because what Moseley needs to demonstrate (but has not demonstrated and cannot demonstrate) is that his own interpretation of Marx’s theory, not the original theory, implies that the rate of profit can change in this case.

 
The New False Claims

I have decided to respond to Moseley’s most recent false claims, even though they are about the irrelevant question he wants to divert the debate onto. I have decided to show that the claims are false, not because they are about something important, but because their falsity helps to disclose that Moseley simply does not know what he’s talking about; and, even worse, that he does not care to know what he’s talking about. That is, he does not take care to verify that his statements are true before he makes them.

To be sure, he’s never lacking for a response. He continues to respond to me by typing longish passages containing lots of technical terms, instead of throwing in the towel and moseleying along. But that doesn’t mean that there are very fine arguments “on both sides,” as Donald Trump might say.

Yet Moseley should not shoulder all of the blame. Ultimately, the problem—as I discussed in the first of my articles that have exposed his failure to demonstrate what he claims­—is that the “Marxian economists” and other left intellectuals have created for themselves a post-truthy environment that fails to enforce and induce norms of decency and scientificity: the need to substantiate what one says, to tell the truth, to refrain from bullshit and lies, and so forth. “Marxian economics means never having to say you’re sorry,” as I’ve put it in the past.

It is this environment that allows behavior like Moseley’s to take place with near-total impunity, and indeed to be rewarded in his “community” and among its devotees. And thus, such behavior continues to take place, again and again.

Moseley’s latest false claims are about an example from Marx that he offered in lieu of any effort to demonstrate the implications of his own interpretation. Moseley notes that, in the example, the various sectors’ compositions of capital (CC) and the uniform rate of surplus value (RS) remain unchanged. He claims, falsely, that this implies that technology and the real wage rate also remain unchanged. And he concludes with the false claim that “CC and RS remain the same, but DC [the distribution of capital] and RP [the rate of profit] change. Therefore, the cause of the change in RP must be a change in DC” (emphasis added), not changes in technology or the real wage rate.

These claims are disproven by the following table.
 
 

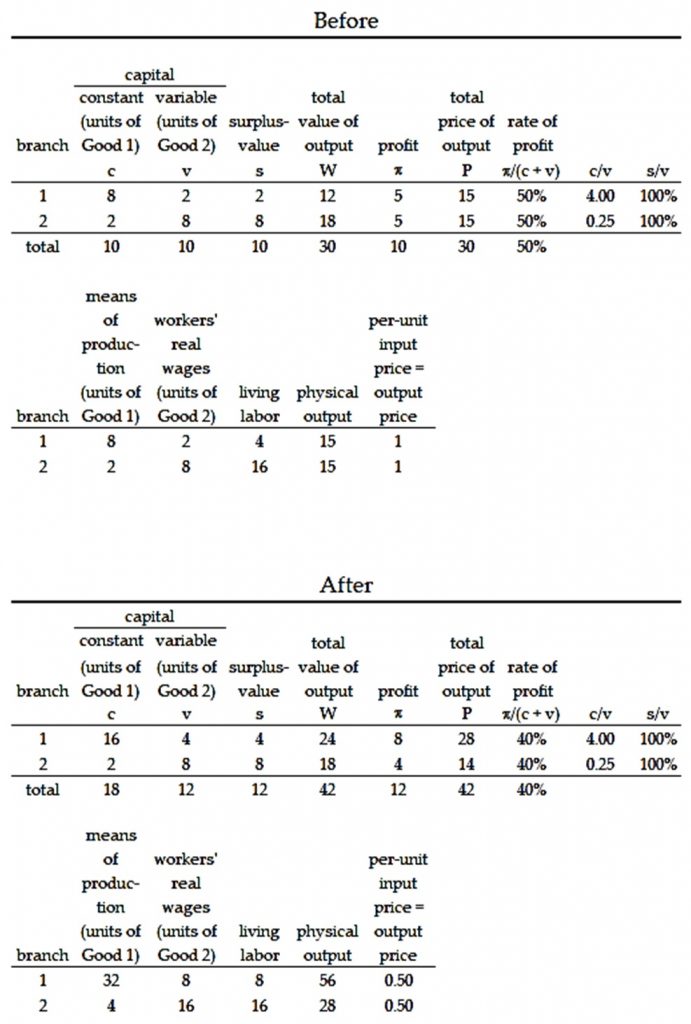
Comparing “Before” and “After,” we see that the value composition of capital (c/v) of each branch remain unchanged, as does the rate of surplus-value (s/v). However, contrary to what Moseley claims, it does not follow that either technology or the real wage rate have remain unchanged. In both branches, there are changes in technology (i.e., in the ratios of means of production to physical output and the ratios of living labor to physical output). And the real wage rate (the ratio of real wages to living labor) doubles.

The change in the rate of profit––its decline from 50% to 40%––is therefore not necessarily caused by the changed distribution of the total advanced capital between the two branches, contrary to what Moseley claims. In principle, the decline might be caused partly by the change in the distribution of capital and partly by the technological changes and/or the rise in the real wage rate. But in fact, the decline is caused exclusively by these latter factors, not by the change in the distribution of capital. If both branches obtain the same rate of profit, per-unit input and output prices are equal, and the technology and real wage ratios are those of the “After” section of the example, then the rate of profit will always be 40%, no matter what the distribution of the total capital between the two sectors may be.

The rates of profit of the two branches, r₁ and r₂, can be expressed as follows:
 

 

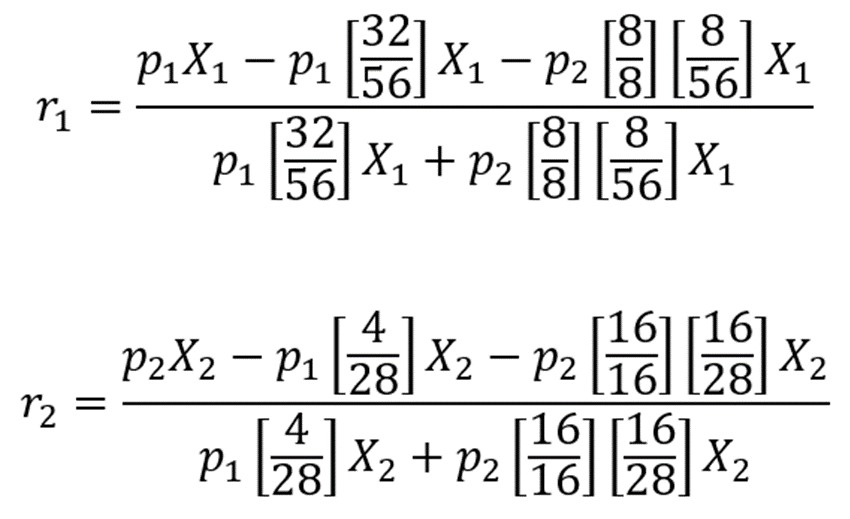
where p₁ and p₂ are the per-unit prices of the goods produced by branches 1 and 2, respectively, and X₁ and X₂ are the quantities of physical output they produce. Since the two rates of profit are equal, by assumption, we can equate the two right-hand side fractions in the equations above. After cross-multiplying, simplifying, etc., we find that p₁ = p₂. Hence, the top equation can be rewritten as 

 

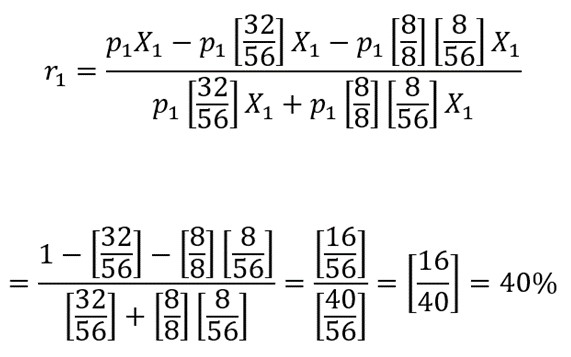
And the second equation can be rewritten as
 
 

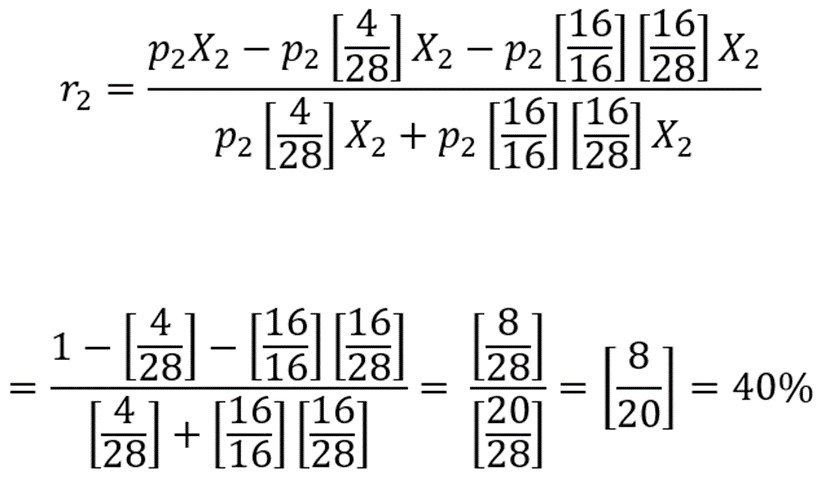
Thus, given that the rate of profit is equalized, per-unit input and output prices are equal, and the technology and real wage ratios are those of my example, the rate of profit must be 40%, no matter what the distribution of the total capital between the two sectors may be. And applying the same procedures to the “Before” section of the example, it is easy to show that the rate of profit there must be 50%, no matter what the distribution of the total capital between the two sectors may be.

How could Moseley have made such obviously false and easily disproven claims? The underlying cause is that, as I indicated above, he does not care to verify that his statements are true before he makes them. There are also proximate causes.

One proximate cause is the fallacy of composition he commits. The term fallacy of composition refers to the incorrect assumption that what is true in individual cases must be true for the whole. It is called a fallacy because it is a logical error that makes the argument that contains it invalid.

Moseley starts by noting that, in his example from Marx, “the composition of capital … remain[s] the same in all industries.” This is correct; in all of the individual cases, the composition of capital remains the same. But he then passes blithely—by means of a fallacy of composition—to the conclusion that the composition of capital in the economy as a whole remains the same:

A change of technology would generally change both the composition of capital and the rate of surplus-value; [but] neither of these determinants of the rate of profit changes …

Furthermore, even if technology or the real wage did change, but had no effect on the composition of capital or the rate of surplus-value (as in Marx’s example), then these changes would not cause the decline in the rate of profit in this example. … The only determinant of the rate of profit that is changing in this example is the distribution of capital ….

Moseley’s line of reasoning is invalid because of his fallacy of composition. In other words, even if the composition of capital remains constant in all individual industries, it might change in the economy as a whole. But how can that be? The answer is simple: industries with a high composition of capital might have become a bigger share of the economy, which would cause the economy-wide composition of capital to rise; or they might have become a smaller share of the economy, which would cause the economy-wide composition to fall.

The example I put forward above illustrates this clearly. In both branches, the composition of capital is unchanged, but in the economy as a whole, the composition of capital rises from 10/10 = 1 to 18/12 = 1.5. This occurs because, in Branch 1, which has a high composition of capital, the value produced and the capital advanced increase, while they remain unchanged in Branch 2, which has a lower composition of capital.[1]

But it gets worse. In addition to the fallacy of composition that Moseley commits, his false claims have a second proximate cause: egregiously sloppy thinking. Note, first of all, that with his (false) conclusion that the economy-wide composition of capital has remained constant, Moseley has “reasoned” himself into a corner. In the example from Marx that he copies, the rate of surplus-value remains constant, and Moseley claims that the economy-wide composition of capital also remains constant. But every change in the rate of profit is attributable to a change in one or both of these factors. If neither of them changes, as Moseley incorrectly alleges, the obvious and inescapable conclusion is that the rate of profit has not changed!

So Moseley is trying to explain why the rate of profit in Marx’s example falls from 22.5% to 13.1%, but his “reasoning” requires him to deny the existence of the phenomenon he’s trying to explain! “What you’re seeing and what you’re reading is not what’s happening.”

But Moseley wants to conclude that what has caused the rate of profit to fall is the change in the distribution of capital, and this conclusion requires him to affirm that it has fallen. So at this point he simply abandons reasoning altogether. He goes straight for what he wants:

CC and RS remain the same, but DC and RP change. Therefore, the cause of the change in RP must be a change in DC. That is my “demonstration”.

But, pray tell, how can the changed distribution of capital (DC) have caused the rate of profit (RP) to fall, even though the economy-wide composition of capital (CC) and the rate of surplus-value (RS) have both remained the same????!!!! Moseley does not tell us.

He does not seem concerned with this teensy-weensy little problem. And without question, he is not concerned enough with the truth-value of his statements to verify that they are true before he makes them. What is important is that he has gotten to the conclusion he wants, and that he has done so at the end of a longish passage containing lots of technical terms that makes it seem as though he knows what he’s talking about. This allows him to get away with calling the passage a “demonstration” and reiterating his false claim about a “difference between my interpretation of Marx’s theory and Sraffian theory.”

I request that Moseley retract the following claims:

1. that the constancy of the rate of surplus-value and the industry-level compositions of capital implies that technology and the real wage rate also remain unchanged;
2. that the economy-wide composition of capital remains the same in the example from Marx that he copied;
3. that the fall in the rate of profit in Marx’s example must be caused by the change in the distribution of capital;
4. that the fall in the rate of profit in Marx’s example cannot be caused, instead or in addition, by changes in technology and the real wage rate;
5. that the economy-wide rate of profit can change even when the economy-wide composition of capital and rate of surplus-value remain constant;
6. that his comment of September 24 exhibits a difference between his interpretation of Marx’s theory and Sraffian theory; and
7. that his comment contains a “demonstration” of one or more of its claims.

 

Bait and Switch Redux

Now we come to the more important problems with Moseley’s reply. One is that it employs the same bait-and-switch stratagem that I exposed and criticized in my first article.

The short version of the story is that, although the claim he needed (and still needs) to demonstrate is a claim about his interpretation of Marx’s value theory, Moseley carefully evaded any examination of the actual implications of his interpretation. Instead, he copied an example of Marx’s, and went on to discuss that example and its implications. As I noted, what he provided was “100% about Marx’s theory and 0% about Moseley’s interpretation.” But then came his bait and switch:

Thus there is a clear difference between my interpretation of Marx’s theory and Sraffian theory [… regarding] the effect of a change in the distribution of capital on the rate of profit. [emphasis added]

After exposing the bait and switch, I pointed out the obvious:

it’s totally illogical to draw a conclusion about Moseley’s interpretation from a set of premises that are not about that interpretation, but instead about Marx’s own theory. Thus, it should be obvious that Moseley has failed to demonstrate his claim, exactly as I predicted.

Well, he’s back to his old tricks. Marxian economics means never having to say you’re sorry for your trickery.

Specifically, every word of Moseley’s comment of September 24 is, until the very end, 100% about Marx’s theory and 0% about Moseley’s interpretation:

Kliman does not mention two crucial details in Marx’s example ….

Furthermore, even if technology or the real wage did change, but had no effect on the composition of capital or the rate of surplus-value (as in Marx’s example) ….

The rate of profit function in Marx’s macro theory of the rate of profit ….

In Marx’s example, CC and RS remain the same, but DC and RP change. Therefore, the cause of the change in RP must be a change in DC. That is my “demonstration”.

Yet immediately thereafter, Moseley writes,

So this is another difference between my interpretation of Marx’s theory and Sraffian theory, in which the distribution of capital has no effect on the rate of profit.

This bait and switch is as unobtrusive as his earlier one. That is, it “isn’t at all unobtrusive—to you and me. But if you’re in a coma or can’t read English, then it probably is unobtrusive.” And it is just as illogical as it was before to draw a conclusion about Moseley’s interpretation from a set of premises that are not about that interpretation, but instead about Marx’s own theory.

So even if Moseley’s latest comment had demonstrated something about Marx’s theory—which it most certainly did not!––it demonstrates absolutely nothing about the implications of Moseley’s interpretation of that theory. It therefore provides no support whatsoever for his claim regarding a difference between his interpretation and Sraffian theory.

 
Moseley’s Smokescreen

The other important problem with Moseley’s reply is that it functions as a smokescreen, drawing attention away from the real issues in this debate, which pertain to the implications of Moseley’s interpretation of Marx’s theory, not to the properties of the original theory. It has become increasingly clear that Moseley does not want to engage in a serious discussion of the implications of his interpretation; and I know why.

To substantiate the smokescreen charge, I will first consider the manner in which his latest comment addresses the second of my articles, to which it is a reply. Moseley begins by saying that “In his latest comment,[2] Kliman argues that my example (taken from Marx) is too general and incomplete and the change in the rate of profit could be due to technological change and/or a change in the real wage.”

Actually, that argument is contained in my first article. In my second article, the one to which Moseley is supposedly replying, I refer to technology and the real wage only incidentally, by quoting from the first article. The full quote is

the example is far too general and incomplete to count as an example of Moseley’s interpretation or to test the truth-value of his recent claim. The numbers he provides are compatible with scenarios in which, contrary to his interpretation, input and output prices aren’t equal, and in which, contrary to his claim, technology and/or the real wage rate are changing and producing the change in the rate of profit.

Moseley’s reply to my second article does not discuss or even mention the other aspect of this quotation, my contention that “[t]he numbers he provides are compatible with scenarios in which, contrary to his interpretation, input and output prices aren’t equal.” But that is the issue I was concerned with––when I quoted this passage, and throughout the second article.

Why does he not address that issue? The answer cannot be that he is unaware of it. Nor can it be that he thinks it is not important enough to address. Why not? Because my discussion of the equality of input and output prices in the second article was a direct response to what Moseley himself recently claimed about that very equality!

The background is this. In my first article, I noted that Moseley claims that his interpretation of Marx’s value theory implies that changes in the distribution of capital cause the rate of profit to change. And I explained why an example that succeeds in demonstrating this claim about the implications of his interpretation must be one in which “THE PER-UNIT PRICES OF OUTPUTS EQUAL THE PER-UNIT PRICES OF INPUTS,” because that equality is an aspect of his interpretation.

Moseley responded by trying to relieve himself of the burden of providing an example in which input and output prices are equal. He argued that this equality “has nothing to do with” the determination of the magnitude of the rate of profit, because his interpretation implies that the rate of profit is determined “prior to and independent of” the establishment of prices of production. Hence, the magnitude of the rate of profit is not altered when he subsequently imposes the equality between input and output prices.

My second article utterly demolished this argument. First, I pointed out a fatal error in its logic:

This second unsubstantiated claim is rather similar to a manufacturer of bottled water claiming that his product is 100% pure and unadulterated because the water flows directly from mountain streams into his company’s holding tanks “prior to and independent of” the bottling process. Because the water is captured before it is bottled, it follows that the fact that his holding tanks were previously used to store toxic sludge “has nothing to do with” the purity of the company’s water!

Moseley has not responded to this challenge to the logic of his argumentation. He has avoided doing so––by talking instead about technology and real wages, and by once again diverting the debate onto a discussion of the properties of Marx’s original theory and away from what he should be talking about, the implications of his own interpretation. Why is he diverting the debate in these ways? Why does he not reply directly to my challenge to his reasoning? Might it be that he has no reply?

In my second article, I went on to note that it is possible, in principle, that Moseley’s “nothing to do with” claim is correct. But I emphasized that he needs to put up or shut up:

Moseley bears the burden of demonstrating that the input price = output price equality doesn’t affect the allegedly predetermined magnitude of the rate of profit. Simply making an unsubstantiated claim that the equality has no effect on the rate of profit, as he has done, is just engaging in a dodge, an attempt to avoid the burden of demonstrating the original unsubstantiated claim.

In the absence of an honest-to-goodness demonstration, we have no reason to accept the claim that the equality of input and output prices doesn’t affect the rate of profit … just like we have no reason to accept an unsubstantiated claim that holding water in tanks contaminated by toxic sludge doesn’t affect the water’s purity.

But Moseley has not “put up.” In other words, he has not demonstrated that his input price = output price equality has no effect on the allegedly predetermined magnitude of the rate of profit. This doesn’t surprise me. It is exactly what I predicted in my second article.

But unfortunately, Moseley has also not “shut up.” Instead of withdrawing this still-unsubstantiated (and still-false) claim, he has chosen to keep it alive by hiding it behind a smokescreen of false blather about the implications of an irrelevant example of Marx’s.

But hey, Marxian economics means never having to substantiate your claims and never having to withdraw them when you can’t substantiate them.

 

Notes

[1] This does not imply that the change in the distribution of capital is a cause of the change in the rate of profit. As I noted above, the rate of profit would fall to 40%, given the changed technology and real wage ratios, even if the distribution of capital remained constant. Conversely, if the distribution of capital changed, but the technology and real wage ratios continued to be those of the “Before” section of my example, the rate of profit would remain at 50%.

Let me also add that I have made absolutely no claims about whether the example I have put forward is in keeping with either Marx’s value theory or with Moseley’s interpretation of that theory. For example, I am not claiming that Marx’s rate of profit is determined physically, nor that his (output) prices of production have to equal the input prices of the same period. Instead, the example shows that the value and price magnitudes in my example, and Marx’s—especially the unchanged branch-level compositions of capital and uniform rate of surplus-value––are compatible with a state of affairs in which the technology and real wage ratios change and cause the rate of profit to change. That is all.

[2] Sic. It is not a comment, but an article. Moseley has placed his replies to my recently published articles at the bottom of a comments section of a different article that was published more than two and a half years ago (go figure). But my recent articles do not appear in that or any other comments section.

 
 
Moseley’s Comment of September 24, 2019

MY DEMONSTRATION

In his latest comment, Kliman argues that my example (taken from Marx) is too general and incomplete and the change in the rate of profit could be due to technological change and/or a change in the real wage.

But Kliman does not mention two crucial details in Marx’s example that suggest that technology and the real wage have not changed – *both the composition of capital and the rate of surplus-value remain the same in all industries*. A change of technology would generally change both the composition of capital and the rate of surplus-value; so the fact that neither of these determinants of the rate of profit changes suggests that technology has not changed. Similarly, a change in the real wage would generally change the rate of surplus-value; so the fact that the rate of surplus-value has not changed suggests that the real wage has not changed.

Furthermore, even if technology or the real wage did change, but had no effect on the composition of capital or the rate of surplus-value (as in Marx’s example), then these changes would not cause the decline in the rate of profit in this example. Technology and the real wage affect the rate of profit only through their effects on the composition of capital or the rate of surplus-value. The only determinant of the rate of profit that is changing in this example is the distribution of capital which must be the cause of the decline in the rate of profit.

The rate of profit function in Marx’s macro theory of the rate of profit could be written in general terms as:

RP = f (CC, RS, DC)              where DC in the distribution of capital

In Marx’s example, CC and RS remain the same, but DC and RP change. Therefore, the cause of the change in RP must be a change in DC. That is my “demonstration”.

So this is another difference between my interpretation of Marx’s theory and Sraffian theory, in which the distribution of capital has no effect on the rate of profit.